扫描关注微信
目前分布式光伏系统的应用主要以工业、商业或民用建筑屋顶为主，光伏阵列排布在分布式系统设计中是非常重要的环节，对于阵列前后间距的优化，我们一般以冬至日上午9时和下午15时阵列前后互不遮挡的原则作为参考，它不仅要考虑当地纬度下的太阳高度角、太阳方位角、安装倾角，也还要考虑屋面本身的坡度、坡面朝向和坡面方位角，而目前对于光伏阵列前后间距的研究文献大多是正南朝向的水平屋面，虽然也有涉及到坡角和方位角，但分析仍不够全面，存在一定的局限性。因为实际的屋面可能同时呈现坡度和方位角，也有可能屋顶坡面东西朝向或主坡副坡同时存在，因此有必要对这些复杂屋面的阵列间距做深入分析。
通常情况下，屋面一般按其坡度的不同分为坡屋面（屋面排水坡度大于10%）和平屋面（屋面排水坡度小于5%）两大类。对于平屋面，一种是只有横向排水坡度（或称为主坡），没有纵向排水坡度（或称为副坡、边坡），另一种则稍复杂些，同时存在主坡和副坡，副坡和主坡形成一定的角度，两种情况参考图1和图2。主坡较常见的为2%~3%，副坡为0.5%～1%。
从光伏组件安装应用角度，目前使用最广泛的为平屋面，如工业彩钢瓦屋面、混凝土屋面，而坡屋面主要为别墅类，因坡屋面自身坡度较高，所以光伏组件一般沿着屋面平铺，参照图3。而平屋面的坡角较小，则需要设计一定的安装倾角来获得更高的发电效率，参照图4。
平屋面可分为坡角为0°角和不为0°角两种，按照坡面朝向又可以分为东西坡和南北坡屋面，如图5为东西朝向双坡面，图6为南北朝向双坡面，这两种屋面光伏阵列朝南安装在南坡或北坡。当然这两种屋面可能同时存在主坡和副坡，也可能存在一定的方位角，为计算方便起见，这里坡面的方位角定义为坡面法线方向在水平面的投影和正南方向的夹角，偏西为正，偏东为负。
本文主要研究对象为东西坡和南北坡这两种典型的平屋面，并推广到屋面含有方位角和主副坡共存的复杂情形。目前阵列前后间距值的获得有理论计算法和软件模拟法，软件法如借助于PVSYST软件，通过对屋面和阵列的建模，输入一系列间距值以可视化的形式模拟阴影变化，再通过不断逼近优化获得符合要求的阵列间距值，其优点是可视化较强，缺点是过程较为繁琐，并且屋面复杂程度越大，软件的模拟难度也会增加，一般可作为辅助分析工具，另一种就是本文重点研究的理论计算法，从模型建立和立体几何上的三角关系入手探索阵列间距和其影响因素之间的本质关系。
在分析上述两种屋面阵列前后间距之前需要先回到水平屋面模型上来，如图7为水平面阵列间距的计算模型，相关参数已在图中标注，具体可参考相关文献。在这里我将三棱锥BCDA和三角形AFE称为水平面上的前后间距计算基础模型，这两个模型非常有用，是复杂坡屋面分析的基础。其中面BCD为水平面，A点为组件的最高点，若组件为纵向安装，则最高点在长边框上，若组件横向安装，则最高点在短边框上，这里以纵向安装为例进行分析。B为A点在水平面上的正投影，太阳光线经过A点与水平面交与D点。BD为AD在水平面上的正投影，CD为BD在正南方向的正投影，太阳高度角∠α=∠BDA，太阳方位角∠β=∠BDC，阵列前后的绝对间距为d，那么d可以表示为：
图7水平面上阵列间距计算经典模型
在水平面阵列间距计算经典模型的基础上，下文依次对上述两种典型坡向的平屋面进行详细分析，第一种是南北坡面，第二种为东西坡面，然后再推广到含有坡面方位角变量的通解公式。
1、平屋面南北坡向（坡面方位角
为0°），坡角θ不为0°
为0°），坡角θ不为0°示意图参考上文图5，这里以南坡为例进行分析。这里分析的方法是将光线和前后阵列组件作南北向的投影，如图8所示。假设某一时刻太阳的方位角为β，高度角为α，组件与屋面夹角γ，屋面坡角θ，光线经过组件的最高点A，与假想水平面相交于E点，与屋面相交于M点。B为组件最高点在水平面的正投影，AQ⊥屋面，|QM|为需要求解的阵列前后的绝对间距d，|FM|为阵列前后的间距（或称中心距），|FQ|为组件在屋面上的投影距离，则可将问题转化到△FAE和△AQM中求解，那么阵列前后间距则为：|FM|=|FQ|+|QM|。
图8南坡斜屋面阵列前后间距模型（立面图）
假设组件长度|AF|=l1，△AFE中，根据水平面基础模型可知，|BE|=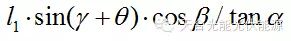
，在△AQM中，根据三角关系：
得
（3）
代入（3）得
则
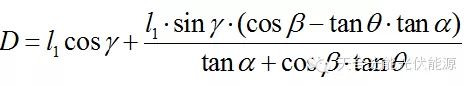（4）
同理，当屋面倾角向下时，也可推导得出：
（4）和（5）合并得：
（适用条件：屋面正南朝向，当屋面倾角向下θ为负，倾角向上θ为正），对于冬至日，阵列间距一般性以上午9点或下午15点的太阳位置进行计算。
【推广公式】坡面非南北朝向（坡面方位角Ƹ不为0°），坡角θ不为0°
上面推导是假设屋面方位角为0°时的情况，实际屋面方位角可能往南偏东或偏西方向。如果是水平屋面，若方位角发生偏移，组件排布仍可以选择正南朝向安装，也可以和屋面方位角保持一致，具体需要视方位角大小对发电量的影响程度而定，但是斜屋面坡面不同，若方位发生偏移，则组件阵列需要同时跟着偏移。
因此如果建筑物坡面有一定的方位角Ƹ，假如南偏西Ƹ，对于冬至日，则需要使用15: 00 的太阳方位角计算，若坡面方位角为南偏东Ƹ，则用9: 00 的太阳方位角计算，所以阵列前后间距计算需要的实际方位角大小应为：
通解D的推广公式可表达如下：
（以水平面作基准面，当屋面坡角向下θ为负，向上θ为正）。
2、坡面东西朝向（坡面方位角Ƹ=±90°），坡角θ不为0°
参考图10和图11，这里先以东坡面（坡面方位角Ƹ=-90°）为例进行分析，组件阵列安装在东坡面，阵列方位角正向朝南，B为组件最高点A的重心线与屋面的交点，O为A在屋面上的垂足，屋面的坡角为θ，则∠BAO也为θ。在图12中，△BEG为假想水平面，棱锥ABEG构成了刚才提到的基础模型，其中BE为太阳光线在△BEG平面上的投影，EG为正南方向的线段，∠AEB为太阳高度角，∠BEG为太阳方位角，阵列与屋面夹角γ，组件长度l1。光线过E与屋面交于D，作AG的延长线交于屋面于C，则DC长度为我们需要求解的阵列前后绝对间距d。
图10 东西坡阵列前后间距分析示意图
图11东西坡阵列前后间距分析（南立面图）
根据图10和图11三角关系得
，其中
；
在图12中，根据水平面基础模型，可得
；
；
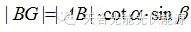从图12几何平行关系，可得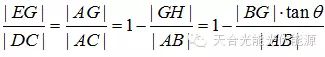
（9）
在△ABC中，
（10）
代入（9）式可得：
所以从（9）式可以求得
（12）
最后阵列前后间距D=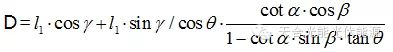
（13）
同理，西坡面阵列前后间距也可求得：
合并（13）和（14）式，可得：
（东坡面：θ为正，西坡面：θ为负）。
【推广公式】坡面非东西朝向，屋面倾角θ不为0°，坡面方位角≠±90°
≠±90°
（坡面南偏东：θ为正，坡面南偏西：θ为负）
3、主副坡同时存在的情况
主副坡同时存在于东西坡面或南北坡面，这在混凝土平屋面上是比较常见的，如图13和图14，这两种情况比上述第1点和第2点还要复杂，这里分析的方法是分为两步，先分析东西向坡面，再在此基础上分析南北向坡面，比如说主坡东西向，副坡南北向，那么就可以按照下面思路去求解：
假设主坡坡角为θ，副坡坡角为Ψ。
根据上述第2点分析出来的公式，可求解出东西坡阵列前后绝对间距d，得到这个值后，进入第二步，如图15在三角形FAE中，|BE|为d，代入第1点所讲的斜面公式，可求解d’。
图15 主副坡情况阵列间距平面分析模型
（其中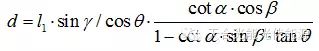 
）；
那么
（18）
（东主坡面：θ为正，西主坡面：θ为负；南副坡面Ψ为正，北副坡面Ψ为负）
同理，对于主坡面南北朝向，副坡东西向：
（其中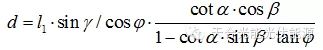 
）；
（南主坡面：θ为正，北主坡面：θ为负；东副坡面Ψ为正，西副坡面Ψ为负）
小结
由于目前光伏屋顶多种多样，有简单也有复杂，稍微简单些的屋面如水平屋面，稍微复杂的如南北坡面和东西坡面，更复杂些存在一定方位角或同时存在主副坡面等等，这些在光伏应用中经常遇到，本文对此进行了详细的阐述和分析，推导出的阵列间距计算公式，可结合使用EXCEL，输入公式中涉及的相关变量就可进行快速计算，而不在本文研究范围的复杂屋面的分析其实也可以参考本文的思路进行研究。 
宁德时代吴凯...
天合光能陈奕...
刘岩: 追光行...
黄震院士：大...